Catatan Disain dan Analisis Keamanan jaringan 6

KRIPTOGRAFI ASIMETRIS

1. Pendahuluan

Pada pertengahan tahun 70-an Whitfield Diffie dan Martin Hellman menemukan teknik enkripsi asimetris yang merevolusi dunia kriptografi.

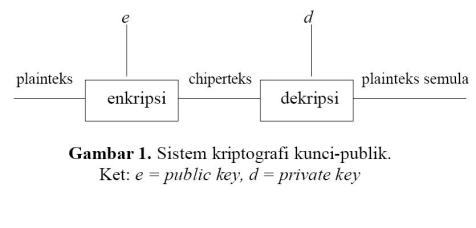
Pada sistem kriptografi kunci-publik, kunci kriptografi dibuat sepasang, satu kunci untuk enkripsi dan satu kunci untuk dekripsi (Gambar 1);

• Kunci untuk enkripsi diumumkan kepada publik – oleh karena itu tidak rahasia – sehingga dinamakan kunci public (public-key), disimbolkan dengan e.
• Kunci untuk dekripsi bersifat rahasia – sehingga dinamakan kunci privat (private key), disimbolkan dengan d.
• Karena ada kunci enkripsi ¹ kunci dekripsi, maka system kriptografi kunci-publik kadang-kadang disebut juga system kriptografi asimetri.

Sistem kriptografi kunci-publik didasarkan pada fakta:

1. Komputasi untuk enkripsi/dekripsi pesan mudah dilakukan.
2. Secara komputasi hampir tidak mungkin (infeasible) menurunkan kunci privat, d, bila diketahui kunci publik, e, pasangannya.

2. Kriptografi Asimetris

Algoritma asimetris (asymmetric algorithm) adalah suatu algoritma dimana kunci enkripsi yang digunakan tidak sama dengan kunci dekripsi. Pada algoritma ini menggunakan dua kunci yakni kunci publik (public key) dan kunci privat (private key). Kunci publik disebarkan secara umum sedangkan kunci privat disimpan secara rahasia oleh si pengguna. Walau kunci publik telah diketahui namun akan sangat sukar mengetahui kunci privat yang digunakan.

Gambar 2. Diagram proses enkripsi dan dekripsi algoritma asimetris

Pada umumnya kunci publik (public key) digunakan sebagai kunci enkripsi sementara kunci privat (private key) digunakan sebagai kunci dekripsi.

Kunci Simetris vs Kunci Asimetris

Secara konsep perbedaan kunci simetris dan asimetris dapat terlihat pada gambar berikut:

Konsep Kriptografi Kunci-Publik (Kriptografi asymmetric)

Konsep kriptografi kunci-publik sederhana dan elegan, tetapi mempunyai konsekuensi penggunaan yang hebat.

• Misalkan E adalah fungsi enkripsi dan D adalah fungsi dekripsi. Misalkan (e, d) adalah pasangan kunci untuk enkripsi dan dekripsi sedemikian sehingga:

Ed(m) = c dan Dd(c) = m

untuk suatu plainteks m dan cipherteks c.

• Kedua persamaan ini menyiratkan bahwa dengan mengetahui e dan c, maka secara komputasi hampir tidak mungkin menemukan m. Asumsi lainnya, dengan mengetahui e, secara komputasi hampir tidak mungkin menurunkan d.
• Ee digambarkan sebagai fungsi pintu-kolong (trapdoor) satuarah dengan d adalah informasi trapdoor yang diperlukan untuk menghitung fungsi inversinya, D, yang dalam hal ini membuat proses dekripsi dapat dilakukan.

Konsep di atas menjadi penting bila kriptografi kunci-publik digunakan untuk mengamankan pertukaran pesan dari dua entitas yang berkomunikasi. Contoh:

Misalkan Alice berkomunikasi dengan Bob. Bob memilih pasangan kunci (e, d). Bob mengirimkan kunci enkripsi e (kunci publik) kepada Alice melalui sembarang saluran tetapi tetap menjaga kerahasiaan kunci dekripsinya, d (kunci privat).

Kemudian, Alice ingin mengirim pesan m kepada Bob. Alice mengenkripsikan pesan m dengan menggunakan kunci public Bob, untuk mendapatkan c = Ee(m), lalu mengirimkan c melalui saluran komunikasi (yang tidak perlu aman). Bob mendekripsi cipherteks c dengan menggunakan kunci privatnya untuk memperoleh m = Dd(c).

Gambar 5. Enkripsi/dekripsi dengan kriptorafi kunci-publik.

Sistem kriptografi kunci-publik juga cocok untuk kelompok pengguna di lingkungan jaringan komputer (LAN/WAN). Setiap pengguna jaringan mempunyai pasangan kunci public dan kunci privat yang bersuaian. Kunci publik, karena tidak rahasia, biasanya disimpan di dalam basisdata kunci yang dapat diakses oleh pengguna lain. Jika ada pengguna yang hendak berkirim pesan ke pengguna lainnya, maka ia ia perlu mengetahui kunci publik penerima pesan melalui basisdata kunci ini lalu menggunakannya untuk mengenkripsi pesan. Hanya penerima pesan yang berhak yang dapat mendekripsi pesan karena ia mempunyai kunci privat.

Dengan sistem kriptografi kunci-publik, tidak diperlukan pengiriman kunci privat melalui saluran komunikasi khusus sebagaimana pada sistem kriptografi simetri.

Meskipun kunci publik diumumkan ke setiap orang di dalam kelompok, namun kunci publik perlu dilindungi agar otentikasinya terjamin (misalnya tidak diubah oleh orang lain).

Kelebihan dan kekurangan Kriptografi asimetris

Kelebihan :

1. Masalah keamanan pada distribusi kunci dapat lebih baik
2. Masalah manajemen kunci yang lebih baik karena jumlah kunci yang lebih sedikit.
3. Hanya kunci privat yang perlu dijaga kerahasiaannya oleh setiap entitas yang berkomuniaksi (tetapi, otentikasi kunci publik tetap harus terjamin). Tidak ada kebutuhan mengirim kunci kunci privat sebagaimana pada system simetri.
4. Pasangan kunci publik/kunci privat tidak perlu diubah, bahkan dalam periode waktu yang panjang.
5. Dapat digunakan untuk mengamankan pengiriman kunci simetri.
6. Beberapa algoritma kunci-publik dapat digunakan untuk memberi tanda tangan digital pada pesan (akan dijelaskan pada materi kuliah selanjutnya)

Kelemahan :

1. Enkripsi dan dekripsi data umumnya lebih lambat daripada sistem simetri, karena enkripsi dan dekripsi menggunakan bilangan yang besar dan melibatkan operasi perpangkatan yang besar.
2. Ukuran cipherteks lebih besar daripada plainteks (bisa dua sampai empat kali ukuran plainteks).
3. Ukuran kunci relatif lebih besar daripada ukuran kunci simetri.
4. Karena kunci publik diketahui secara luas dan dapat digunakan setiap orang, maka cipherteks tidak memberikan informasi mengenai otentikasi pengirim.
5. Tidak ada algoritma kunci-publik yang terbukti aman (sama seperti block cipher). Kebanyakan aalgoriam mendasakan keamanannya pada sulitnya memecahkan persoalan-persoalan aritmetik (pemfaktoran, logaritmik, dsb) yang menjadi dasar pembangkitan kunci.

Aplikasi Kriptografi Kunci-Publik

Aplikasi kriptogafi kunci-publik dapat dibagi menjadi 3 kategori:

1. Enkripsi/dekripsi

Seperti pada algoritma kriptografi simetri, algoritma kunci-publik dapat digunakan untuk menjaga kerahasiaan pesan (provide confidentiality/secrecy). Contoh algoritma: RSA, Knapsack, Rabin, ElGamal

2. Digital signatures

Algoritma kriptografi kunci-publik dapat digunakan untuk membuktikan otentikasi pesan maupun otentikasi pengirim (provide authentication) Contoh algoritma: RSA, DSA, ElGamal, GOST

3. Pertukaran kunci (key exchange)

Algoritma kriptografi kunci-publik dapat digunakan untuk pengiriman kunci simetri (session keys) Contoh algoritma: RSA, Diffie-Hellman

Beberapa algoritma kriptografi kunci-publik cocok digunakan untuk ketiga macam kategori aplikasi (misalnya RSA), beberapa algoritma hanya ditujukan untuk aplikasi spesifik (misalya DSA untuk digital signature).

• DSA untuk digital signature

Tandatangan digital seperti halnya tandatangan biasa digunakan untuk membuktikan keaslian dari suatu dokumen yang dikirimkan. Kunci privat digunakan untuk menandatangani, sedangkan kunci publik digunakan untuk membuktikan keaslian tandatangan itu.

Untuk lebih memudahkan pengertian tandatangan digital dapat diilustrasikan sebagai berikut :

Untuk menandai pesannya, si Pengirim menyandi pesan tersebut dengan kunci privat-nya. Setiap orang yang memiliki pasangan kunci publik-nya dapat membuka pesan tersandi itu dan mengetahui dengan pasti si Pengirim adalah orang yang tepat. Cara ini tidak melindungi kerahasiaan datanya, mengingat setiap orang dapat saja memiliki pasangan kunci publik dari si Pengirim. Tujuan dari tandatangan digital hanyalah membuktikan bahwa pesan tersebut memang dari si Pengirim.

Sifat yang diinginkan dari tanda tangan digital diantaranya adalah:

1. Tanda tangan itu asli (otentik), tidak mudah ditulis/ditiru oleh orang lain. Pesan dan tanda tangan pesan tersebut juga dapat menjadi barang bukti, sehingga penandatangan tak bisa menyangkal bahwa dulu ia tidak pernah menandatanganinya.
2. Tanda tangan itu hanya sah untuk dokumen (pesan) itu saja. Tanda tangan itu tidak bisa dipindahkan dari suatu dokumen ke dokumen lainnya. Ini juga berarti bahwa jika dokumen itu diubah, maka tanda tangan digital dari pesan tersebut tidak lagi sah.
3. Tanda tangan itu dapat diperiksa dengan mudah.
4. Tanda tangan itu dapat diperiksa oleh pihak-pihak yang belum pernah bertemu dengan penandatangan.
5. Tanda tangan itu juga sah untuk kopi dari dokumen yang sama persis.

Meskipun ada banyak skenario, ada baiknya kita perhatikan salah satu skenario yang cukup umum dalam penggunaan tanda tangan digital. Tanda tangan digital memanfaatkan fungsi hash satu arah untuk menjamin bahwa tanda tangan itu hanya berlaku untuk dokumen yang bersangkutan saja. Bukan dokumen tersebut secara keseluruhan yang ditandatangani, namun biasanya yang ditandatangani adalah sidik jari dari dokumen itu beserta timestamp-nya dengan menggunakan kunci privat. Timestamp berguna untuk menentukan waktu pengesahan dokumen.

• Metoda RSA ( Rivest, Shamir, Adleman )

RSA adalah kriptografi kunci public ( public key ) yang dapat dipergunakan untuk melakukan proses enkripsi dan juga otentikasi ( dengan digital signature ).
Proses enkripsi menggunakan metoda RSA ini adalah dengan cara mengkodekan karakter ke bentuk numeric, misalnya A diganti menjadi 1, B diganti menjadi 2, C diganti menjadi 3 dan seterusnya.

Kekuatan atau keamanan algoritma ini terletak pada kesulitan untuk menfaktorkan bilangan hasil perkalian dari dua buah bilangan prima yang bernilai besar.
Metoda RSA ini dibuat pada tahun 1978 di MIT ( Massachusets Institute of technology ) oleh Ron Rivest, Adi Shamir, dan Leonard Adleman. Metoda RSA ini telah diterima secara luas oleh produk-produk komunikasi data komersial sebagai pendukung keamanan data.

Algoritma RSA

Kunci Publik:

– n = p*q,  p & q bil. Prima besar dan dirahasiakan

– e relatif prima terhadap F(n)=(p-1).(q-1)

• Kunci Rahasia:

–  d*e=1 mod F(n)àd*e mod F(n)=1

• Enkripsi:

– C = m^(e) mod n

• Dekripsi:

– M = C^(d) mod n

Contoh RSA:

• Kunci Publik:

– Pilih bil. prima p = 7 dan q = 11, n = 7.11 =77

– F(n)=(p-1).(q-1)=6.10= 60 artinya

F(n)={1,2,3,4,6,8,..,76}={x|gcd(x, n)=1}

– Pilih e dalam {x|gcd(x, 60)=1}, misalnya e=17

– Hapus p dan q dan Kunci Publik n=77, e=17

• Kunci Rahasia:

– d = e-1 mod F(n), d *e = 1 mod 60, d =53

– 53 * 17 mod 60 = 901 mod 60 = 1 mod 60

• c = “PESAN”, m = 16 5 19 1 14
• Enkripsi: C = m ^(e) mod n

– C1 = 16^(17) mod 77 = 25

– C2 = 5^(17) mod 77 = 3

– C3 = 19^(17) mod 77 = 24

– C4 = 11^(7) mod 77 = 1

– C5 = 14^(17) mod 77 = 42

• C= 25 03 24 01 42, C = “YCXAp”
• Dekripsi: M = C^(d) mod n

– M1 = 25^(53) mod 77 = 16

– M2 = 3^(53) mod 77 = 5

– M3 = 24^(53) mod 77 = 19

– M4 = 1^(53) mod 77 = 1

– M5 = 42^(53) mod 77 = 14